Null Hypothesis

A statement about population, which is tested on sample of population and rejected if does not satisfy the required level of statistical significance is called Null Hypothesis.

When Null Hypothesis is rejected, its complementary statement, the Alternate Hypothesis is true for the given sample.

 

The null hypothesis and the alternate hypothesis are terms used in statistical tests, which are formal methods of reaching conclusions or making decisions on the basis of data.

The statement being tested in a test of [statistical] significance is called the null hypothesis. The test of significance is designed to assess the strength of the evidence against the null hypothesis.
Usually, the null hypothesis is a statement of 'no effect' or 'no difference'. It is often symbolized as H0.

The statement that is hoped or expected to be true instead of the null hypothesis is the alternative hypothesis. Symbols include H1 and Ha.

Statistical significance test: "Very roughly, the procedure for deciding goes like this: Take a random sample from the population. If the sample data are consistent with the null hypothesis, then do not reject the null hypothesis; if the sample data are inconsistent with the null hypothesis, then reject the null hypothesis and conclude that the alternative hypothesis is true.

Wikipedia: Null Hypothesis

null-hypothesis-8

null-hypothesis-7

Type I Error & Type II Error

 

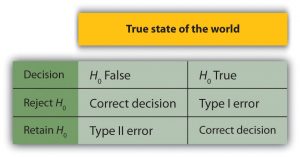
null-hypothesis-3

When null is true:

Type I Error is rejecting the null when it is true (probability = α)

Correct decision is not rejecting the null when it is true (probability = 1- α)

 

When null is false:

Type II Error is failing to reject the null when it is false (probability = β)

Correct decision is rejecting the null when it is false (probability = 1- β)

 

 

Example: Study to see effect of two medicines to treat patients

To see the effect of two medicines the null hypothesis is the default statement that there is no difference between the medicines. To validate this statement null hypothesis testing is done on a sample data of the population. There are two datasets representing two samples for the effect of two medicines and the test  statistic means is used.

 

Null Hypothesis: The two medicines have same effect, that is, the means of two samples are equal.

Null Hypothesis Testing:  (H0): μ1= μ2

 

Alternate Hypothesis: The two medicines have different effect, that is, the means of two samples are not equal.

Alternate Hypothesis Testing: (H1): μ1≠ μ2

 

Type I error occurs when the study rejects the null hypothesis and concludes that the two medicines are different when actually they have the same effect.

Consequence of Type I error: Rejecting a medicine as less effective is not that big a problem because patients have at least one medicine for treatment.

 

Type II error occurs when the study fails to reject the null hypothesis and concludes that both the medicines are effective in treating the patients when actually one of them is not.

Consequence of Type II error: Not rejecting a medicine that can not treat patients can cost patients their life as such this error is not acceptable.

 

Evaluating the Risk of Type I error and Type II error

Depending on which error costs more the level of tolerance called significance is set while testing the null hypothesis using a particular statistic.

 

P-value ( p )

Probability Value is the probability of the statistic used to test the null hypothesis. p-value along with probability of occurrence of type I and type II errors determines whether to reject or not reject the null hypothesis.

 

Significance ( α )

Is the acceptable level of Type I error denoted as α. Say a 5 percent of tolerance is allowed for Type I error beyond which the null hypothesis is rejected. That is out of 20 samples, we're willing to accept one rejection of null hypothesis even if it is true. α can also be 1 percent if consequences of Type I error are costly.

If p-value < α - that is less than tolerance of Type I error - then the null hypothesis is rejected in favor of the alternate hypothesis.

 

Power of Test ( 1-β )

Similarly, the acceptable level of Type II error is denoted as β. β is probability of not rejecting null hypothesis when it is false; so (1-β) is correctly rejecting the null hypothesis when it is false and hence it is called the power of the statistical test.

Typically level of acceptance for type I error α is 5 percent; generally the target for β is 20 percent or 10 percent thus 80 percent or 90 percent is set as the target for power of test.

 

Interpreting the statistical test result:

α = 0.05

p = 0.04

Since p < α  we reject the null hypothesis.

This however, does not mean that there is 4 % probability that null hypothesis is true. It means that assuming null hypothesis is true, the sample data exhibits the statistical test with probability 0.04.

It is conditional probability P(D/H0) = 0.04

D - the event that sample data exhibits the test statistic

 

Critical Region

If the test statistic falls in this region under the normal distribution curve of the sample data the null hypothesis is rejected.

This region is depicted as the extreme value on either the left, right or both sides of the normal curve, that is near the tail.

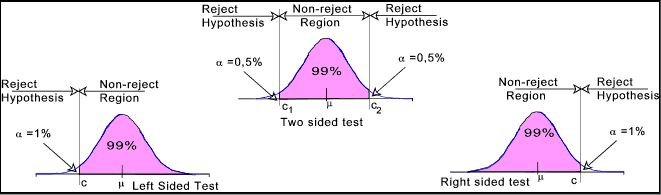
null-3

 

One-Tailed Null Hypothesis Testing

When the critical region ( i.e. null hypothesis rejection region ) is only one side of the normal distribution curve - either left tail or right tail it is called one-tailed null hypothesis.

It is also called directional hypothesis testing because the alternate hypothesis rejects the null hypothesis by comparing the test statistic value to be either greater than or less than the reference value specified in the null hypothesis.

For example:

H0: μ = 20 vs. H1: μ > 20

H0: μ = 200 vs. H1: μ < 300

 

Two-tailed Null Hypothesis Testing

When the critical region ( i.e. null hypothesis rejection region ) is on both sides of the normal distribution curve - left and right tail it is called two-tailed null hypothesis testing.

It is also called non-directional hypothesis testing because the alternate hypothesis rejects the null hypothesis if the test statistic value is not equal to the reference value specified in the null hypothesis - regardless of whether it is greater than or less than the specified value.

For example:

H0: μ = 850 vs. H1: μ≠ 850

 

Null Hypothesis Testing Using R

t.test function is used in R for hypothesis testing

See the one-sample, two-sample and paired-sample t.test examples below.

# see how to use the t.test function

?t.test

# Description

# Performs one and two sample t-tests on vectors of data.

# Usage

# t.test(x, ...)

## Default S3 method:
# t.test(x, y = NULL,
# alternative = c("two.sided", "less", "greater"),
# mu = 0, paired = FALSE, var.equal = FALSE,
# conf.level = 0.95, ...)

# default is two-sided

One-Sample t.test

 

Understanding the Lung Capacity dataset

We load the tab separated data file which has the Lung Capacity dataset.

 

# load lung capacity data
# from text file with tab delimited columns

lungCapacity_df = read.csv("~/dataFiles/LungCapData.txt", header=T, sep="\t")

class(lungCapacity_df)
# [1] "data.frame"

# see the rows and columns in data frame

dim(lungCapacity_df)
# [1] 725 6

str(lungCapacity_df)
# 'data.frame': 725 obs. of 6 variables:
# $ LungCap : num 6.47 10.12 9.55 11.12 4.8 ...
# $ Age : int 6 18 16 14 5 11 8 11 15 11 ...
# $ Height : num 62.1 74.7 69.7 71 56.9 58.7 63.3 70.4 70.5 59.2 ...
# $ Smoke : Factor w/ 2 levels "no","yes": 1 2 1 1 1 1 1 1 1 1 ...
# $ Gender : Factor w/ 2 levels "female","male": 2 1 1 2 2 1 2 2 2 2 ...
# $ Caesarean: Factor w/ 2 levels "no","yes": 1 1 2 1 1 1 2 1 1 1 ...
names(lungCapacity_df)
# [1] "LungCap" "Age" "Height" "Smoke" "Gender" "Caesarean"

# see summary of lung capacity

summary(lungCapacity_df$LungCap)
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# 0.507 6.150 8.000 7.863 9.800 14.680

Boxplot Lung Capacity

 

#boxplot lung capacity

boxplot(lungCapacity_df$LungCap,
col=c("yellow"),
main="Boxplot for Lung Capacity",
ylab="Lung Capacity", las=1)

null-hypo-bplot-lungCap

Interpret the t.test result 

 

Here test statistic is based on single statistic. For example mean of Lung Capacity for the given dataset.

 

Null Hypothesis: Mean of LungCap is greater than 8

H0: μ >= 8 vs. H1: μ < 8

 

# we test with 5 percent significance level
# that is, confidence interval 95 %

Test.one.sided.95 = t.test(lungCapacity_df$LungCap,
mu=8,
alt="less",
conf=0.95)

Test.one.sided.95

# One Sample t-test

# data: lungCapacity_df$LungCap
# t = -1.3842, df = 724, p-value = 0.08336
# alternative hypothesis: true mean is less than 8
# 95 percent confidence interval:
# -Inf 8.025974
# sample estimates:
# mean of x
# 7.863148

names(Test.one.sided.95)
# [1] "statistic" "parameter" "p.value" "conf.int" "estimate"
# [6] "null.value" "alternative" "method" "data.name"

# to reject or not to reject the null hypothesis

p = Test.one.sided.95$p.value

significance = 0.05

Result = ifelse( (p - significance)>0,
"NULL is True",
"Alternate is True: Reject Null" )

Result
# [1] "NULL is True"

 

Independent two-Sample t-test

Here we test the null hypothesis by comparing the test statistics of two populations.

It is way of examining the relationship between a numeric variable Y and a categorical variable with two levels - each level is one sample.

 

Lung Capacity of Non-Smokers Vs Lung Capacity of Smokers

We compare the means of below two populations:
μ1 - mean of lung capacity for smokers
μ2 - mean of lung capacity for non-smokers

Null Hypothesis: Two means are equal

Alternate Hypothesis : Two means are not equal, two-tailed testing

H0: μ1 = μ2 vs. H1: μ1 ≠ μ2

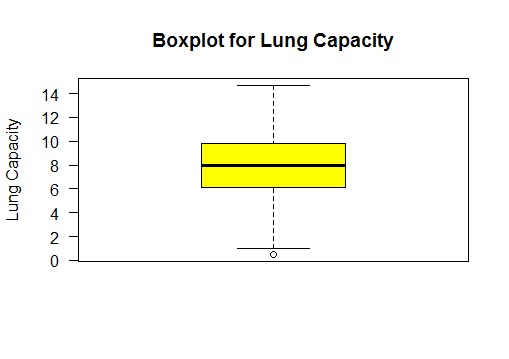
Boxplot the two sample populations 

 

Group 1 : Lung Capacity of Non-Smokers

Group 2 : Lung Capacity of Smokers

 

It shows the lung capacity of non-smokers has higher variance than that of smokers.

 

# lung capacity for smokers and non-smokers

class(lungCapacity_df$LungCap)
#[1] "numeric"

class(lungCapacity_df$Smoke)
#[1] "factor"

summary(lungCapacity_df$LungCap)
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# 0.507 6.150 8.000 7.863 9.800 14.680

summary(lungCapacity_df$Smoke)
# no yes
# 648 77

# box plot lungcapacity wrt to smoker - yes or no

boxplot(lungCapacity_df$LungCap~lungCapacity_df$Smoke)

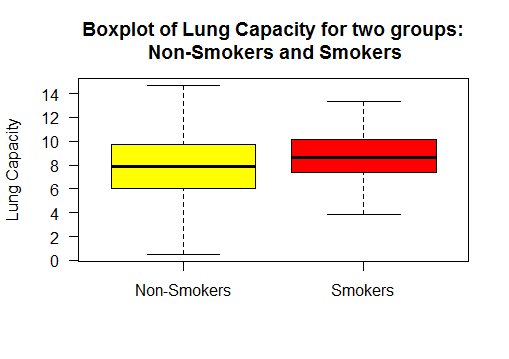
null-hypo-bplot-lungCap-smokers

Interpret result of t.test for 2-samples

 

p value is less than significance 0.05
So we reject null hypothesis for this sample
Alternate hypothesis is true, that is means of two samples is not
equal

# what is variance of the two groups
# that is variance in lungcapacity of smokers and non-smokers

var(lungCapacity_df$LungCap[Smoke=="yes"])
# [1] 3.545292

var(lungCapacity_df$LungCap[Smoke=="no"])
# [1] 7.431694

#so we can see that the lungCap of non-smokers is in wider range than that compared to smokers so in t.test function we specify var.eq as false

t.test(lungCapacity_df$LungCap~lungCapacity_df$Smoke,
mu=0,
alt="two.sided",
var.equal=FALSE)

# Welch Two Sample t-test

# data: lungCapacity_df$LungCap by lungCapacity_df$Smoke
# t = -3.6498, df = 117.719, p-value = 0.0003927
# alternative hypothesis: true difference in means is not equal to 0
# 95 percent confidence interval:
# -1.3501778 -0.4003548
# sample estimates:
# mean in group no mean in group yes
# 7.770188 8.645455

 

Paired t-test

Here the t-test is done on two populations that are dependent on each other.

We use the blood pressure dataset which records the blood pressure of patients before and after treatment.

 

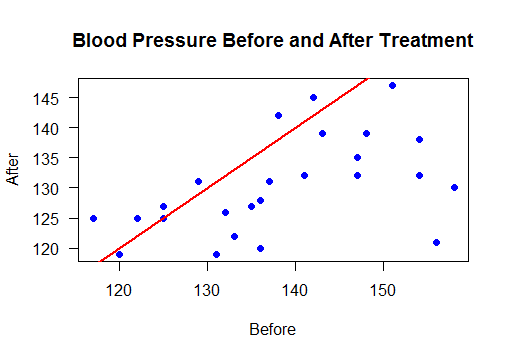
Blood pressure before and after treatment

We compare the means of below two dependent populations:
μ1 - mean of blood pressure before treatment
μ2 - mean of blood pressure after treatment

Null Hypothesis: Two means are equal

Alternate Hypothesis : Two means are not equal, two-tailed testing

H0: μ1 = μ2 vs. H1: μ1 ≠ μ2

Read data from file

Blood pressure data is stored externally in tab delimited text file.

# blood pressure recorded before and after treatment
# read tab separated text file

bloodPressure = read.table("~/BloodPressure.txt", header=T, sep="\t")

dim(bloodPressure)
# [1] 25 3

names(bloodPressure)
[1] "Subject" "Before" "After"

str(bloodPressure)
# 'data.frame': 25 obs. of 3 variables:
# $ Subject: int 1 2 3 4 5 6 7 8 9 10 ...
# $ Before : int 135 142 137 122 147 151 131 117 154 143 ...
# $ After : int 127 145 131 125 132 147 119 125 132 139 ...

summary(bloodPressure)
# Subject Before After
# Min. : 1 Min. :117.0 Min. :119.0
# 1st Qu.: 7 1st Qu.:131.0 1st Qu.:125.0
# Median :13 Median :137.0 Median :130.0
# Mean :13 Mean :138.3 Mean :130.3
# 3rd Qu.:19 3rd Qu.:147.0 3rd Qu.:135.0
# Max. :25 Max. :158.0 Max. :147.0

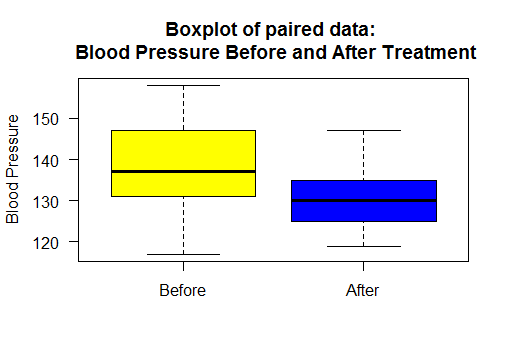
Boxplot and Scatter Plot for paired dataset

 

Boxplot of blood pressure before and after treatment.

 

Scatter plot with regression line
Points below the line show reduced blood pressure after treatement

 

#boxplot

boxplot(bloodPressure$Before, bloodPressure$After,
names=c("Before","After"),
col=c("yellow","blue"),
main="Boxplot of paired data: \n Blood Pressure Before and After Treatment",
ylab="Blood Pressure", las=1)

 

null-hypo-bplot-bp-paired-data

#Scatter plot

plot(bloodPressure$Before, bloodPressure$After,
main="Blood Pressure Before and After Treatment",
xlab="Before", ylab="After",las=1,pch=19, col="blue")

abline(a=0, b=1, col="red",lwd=2)

null-hypo-splot-bp-paired-data

Interpret result of  t.test for two dependent samples

p value is less than significance 0.05 so we reject null hypothesis for this sample.
Alternate hypothesis is true, that is means of two samples is not
equal

# since samples are paired pass paired as true

t.test(bloodPressure$Before,bloodPressure$After,
mu=0,
alt="two.sided",
paired=T,
conf.level=0.99)

# Paired t-test

# data: bloodPressure$Before and bloodPressure$After
# t = 3.8882, df = 24, p-value = 0.0006986
# alternative hypothesis: true difference in means is not equal to 0
# 99 percent confidence interval:
# 2.245279 13.754721
# sample estimates:
# mean of the differences
# 8