K-means Clustering

Unsupervised Learning

The number of clusters 'k' is decided in advance. For each cluster a center point is taken such that the cluster centers are as far away as possible from each other. The data points of the dataset are assigned that cluster for which the cluster center is nearest compared to other cluster centers.

Once all the data points are assigned to clusters based on minimum distance to cluster centers, a new cluster center is calculated for each cluster as the mean of distance of the data points in the cluster from its center. The data points will now be placed in cluster according to the minimum distance from the new cluster center.

This iteration of calculating new cluster center continues until there is no change in cluster center.

kmeans1

kmean-algo-1

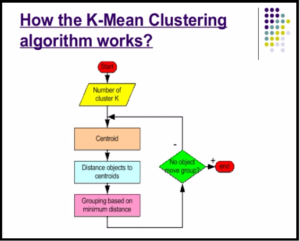
kmean-algo-2

K-Means Clustering Algorithm

How it Works?

By Victor Lavrenko

k-means clustering : how it works

Programming Logic

Steps to cluster data points based on numerical features using KMeans clustering algorithm and compare the results with Hierarchical clustering.

 

Pre-requisite:

Understand the dataset for pre-processing that may be requierd for clustering algorithm.

Step 1:
Remove the categorical variable from the dataset.

Step 2:
Use k-means function for number of clusters.

Step 3:
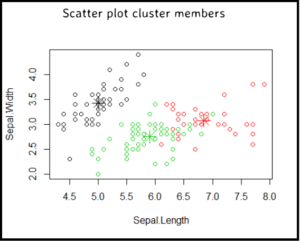
Scatter plot two dimensions colour coding data points per the k-means cluster members. Also plot the cluster centers and interpret the plot.

Step 4:
Compare the cluster members with actual values of the categorical variable.

Step 5:
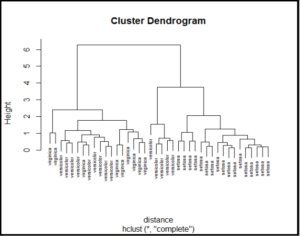
Now use Hierarchical clustering and plot Dendogram

Step 6:
Interpret Dendogram ad compare the with k-means scatter plot for cluster members.

 

Understanding data set

We use the inbuilt dataset iris.

It has 150 observations and 5 variables.

# check dimensions of data set

dim(iris)
# [1] 150 5

names(iris)
#[1] "Sepal.Length" "Sepal.Width" "Petal.Length" "Petal.Width" "Species"

str(iris)
#'data.frame': 150 obs. of 5 variables:
# $ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
# $ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
# $ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
# $ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
# $ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...

Data pre-processing 

We remove the categorical variable 'Species' from the dataset and use remaining four to identify the clusters using k-means clustering.

# now we remove the 'Species' column from the data
# this is to make sure the data is unlabeled

iris_numerical =iris[,-5]
str(iris_numerical)

#'data.frame': 150 obs. of 4 variables:
# $ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
# $ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
# $ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
# $ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...

Identify clusters using k-means

Set k to 3 as the categorical variable Species has three values.

 

# iris dataset contains three classes so we set the cluster number to 3
# use kmeans clustering for 3 clusters

kmeansClustering = kmeans(iris_numerical,3)

kmeansClustering

# K-means clustering with 3 clusters of sizes 50, 62, 38

# Cluster means:
# Sepal.Length Sepal.Width Petal.Length Petal.Width
# 1 5.006000 3.428000 1.462000 0.246000
# 2 5.901613 2.748387 4.393548 1.433871
# 3 6.850000 3.073684 5.742105 2.071053

# Clustering vector:
# [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
# [30] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 3 2 2 2 2 2
# [59] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2
# [88] 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 3 3 3 3 2 3 3 3 3 3 3 2 2 3
# [117] 3 3 3 2 3 2 3 2 3 3 2 2 3 3 3 3 3 2 3 3 3 3 2 3 3 3 2 3 3
# [146] 3 2 3 3 2

# Within cluster sum of squares by cluster:
# [1] 15.15100 39.82097 23.87947
# (between_SS / total_SS = 88.4 %)

# Available components:

# [1] "cluster" "centers" "totss" "withinss"
# [5] "tot.withinss" "betweenss" "size" "iter"
# [9] "ifault"

Scatter plot

Plot two dimensions colour coding the data points based on which KMeans cluster they belong to; and show the cluster centers.

# there are four dimensions to the data but we use only two
# plot Sepal length & width and colour as per cluster
# membership

plot(iris_numerical[c("Sepal.Length","Sepal.Width")],
col = kmeansClustering$cluster)

#plot cluster centers for the clusters

points(kmeansClustering$centers[,c("Sepal.Length", "Sepal.Width")], col =1:3, pch=8, cex=2)

Interpret cluster members scatter plot

Some red points are closer to the green center, this is due to remaining two dimensions viz. Petal.Length and Petal.Width which are not included in the scatter plot.

 

 

 

kmeans-cluster-members

Compare with actual values

Lets compare the cluster members with the actual total values for the categorical attribute.

#Lets compare the kmeans cluster with the Species classes

table(iris$Species, kmeansClustering$cluster)

#                             1          2         3
# setosa                 50       0        0
# versicolor          0         48      2
# virginica            0         14       36

# cluster setosa can be separated from other clusters
# clusters versicolor and virginica have a small degree of overlap

Compare with Hierarchical clustering

We compare the k-means clusters with that of Hierarchical clustering.

 

 

 

# now lets apply hierarchical clustering
# we take a random sample of 40 records to avoid overcrowding

index = sample(1:nrow(iris_numerical), 40)
index
iris_numerical_40 = iris_numerical[index,]
iris_numerical_40

# calculate Ecuclidean distance

distance = dist(iris_numerical_40)
distance
print(distance, digits=3)

iris_numerical_40_hc = hclust(distance)

iris_numerical_40_hc

# Call:
# hclust(d = distance)

# Cluster method : complete
# Distance : euclidean
# Number of objects: 40

Plot Dendogram

See the Hierarchical clusters using dendogram.

# plot dendogram for hierarchical clustering

plot(iris_numerical_40_hc)

# plot(iris_numerical_40_hc, hang=-1, labels=iris$Species[index])

plot(iris_numerical_40_hc, 
                              labels=iris$Species[index],
                                                cex=0.6)

Interpret cluster member dendogram

Similar to k-means cluster here also we can see that setosa can be separated from remaining two clusters, clusters virginca and versicolor are overlapping

 

 

 

iris-hc-cl